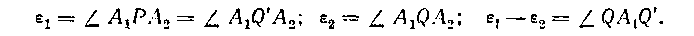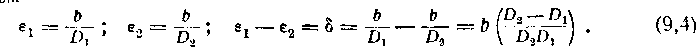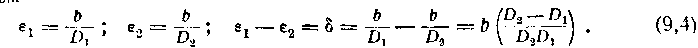
При этом может йредставйтьйй случай, когда расстояния р_ус_л й p₂q₂ одинаковы и расположены в одном направлении в обоих глазах. Восприятие таких изображений дает нам суждение о том, что обе рассматриваемые точки находятся на одинаковом расстоянии от глаз.

Смещение точки Q вдоль прямой линии A₂Q из положения Q' в направлении к глазу или от глаза вызывает для левого глаза смещение изображения д_г из идентичной точки в направлении или к височной части сетчатки или к носовой. Аналогичное рассмотрение для правого глаза (при смещении точки Q из положения Q' вдоль направления А^') показывает, что всякое смещение одного изображения из идентичной точки в височную область сетчатки соответствует приближению предмета и вызывает стереоскопическое восприятие, отмечающее, что предмет Q лежит ближе Р. Всякое смещение одного изображения из идентичной точки в носовую область соответствует удалению предмета и дает стереоскопическое восприятие, отмечающее, что предмет Q лежит дальше Я. В этом заключается, между прочим, объяснение стереоскопического эффекта.

На рис. 168 имеем параллактические углы

От величины последнего из этих углов зависит величина смещения конца изображения из идентичной точки д_г'. Предельный угол QA_}Q', физиологически нами еще воспринимаемый, обозначим через 8. Этот угол и определяет угловую точность стереоскопического восприятия. Из опытов найдено, что для очень большого количества людей угол 8 достигает величины примерно 10".

Обозначим межзрачковое расстояние А₁А₂ через b (в среднем равное 65 мм). Ввиду того, что расстояния до предметов обычно велики по сравнению с расстоянием Ь, дистанция D определяется знакомой нам формулой

где е — параллактический угол, выраженный в радиальной мере.

Пусть мы имеем два предмета с параллактическими углами е_х и е₂; определим такое их наименьшее взаимное удаление, которое мы еще можем физиологически воспринять, т. е. определим ошибку восприятия глубины. Из формулы (9,3) имеем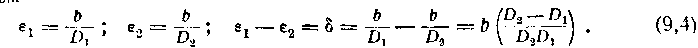

Разность расстояний D₂ — О_г обозначим через dD\ ввиду того, что расстояния эти очень мало отличаются друг от друга (по сравнению с их абсолютной величиной), в знаменателе предыдущей формулы можем принять D, — = D; тогда имеем

т. е. относительная ошибка растет пропорционально дистанции. Ниже, при рассмотрении работы бинокулярных приборов и дальномеров (гл. 24, стр. 207), мы подробно проанализируем формулы (9,6) и (9,7).

Окончательно имеем ошибку в оценке глубины

т. е. ошибка пропорциональна квадрату дистанции. Для относительной ошибки имеем формулу